布莱斯·帕斯卡（1623年6月19日—1662年8月19日） 出版了《论算术三角形》（Traité du triangle arithmétique avec quelques autres petits traités sur la měme matière）。同年，与皮埃尔·费马（1601年8月17日

—1665年1月12日）写就《与费马在概率理论方面的通信集》（Correspondence with Fermat on the Theory of Probabilities），见《西方世界的伟大著作：帕斯卡篇》（Great   Books   of   the   Western   World：Pascal）

（Franklin Library，1984），pp.447~487。

帕斯卡三角形、概率论、点数问题、帕斯卡赌注

最早对组合问题的研究似乎始于印度 ¹。大约在公元1150年，婆什迦罗就认识到了从j个数中取出n个数的组合数为n！/［j！（n－j）！］。早在1265年，阿拉伯数学家图西就知道了二项展开式（a+b） ⁿ的系数计算以及如何在三角形中排列展开式系数。中国数学家朱世杰1303年出版的《四元玉鉴》也讲述了二项展开式的计算，该书的扉页后来广为流传。法国的马林·梅森（1588—1648）在1636年就懂得了组合恒等式与展开式系数之间的对等关系。

帕斯卡虽然不是算术三角形的发明者，但他首次著文将组合数学、二项展开式系数与三角形阵列这三者联系起来。由于帕斯卡对三角形的特征进行了详细深入的探讨，因而从此以后人们将三角形阵列称为帕斯卡三角形。值得指出的是，在论述算术三角形以及点数问题时，帕斯卡并没有直接使用现代概率学的概念，甚至没有用过概率一词。相反，他用的是组合数学语言，比如在多次试验中某某事件发生多少次。因此，后文其实是我用现代化的语言对帕斯卡的研究进行的重新表述。

帕斯卡三角形以1作为首行开始，接下来各行的每位数字等于上一行位于它上方两个数字的和。

帕斯卡指出，三角形具有许多令人惊讶的特征。例如，如果把首行称为第0行，那么第n行的数字正是二项展开式（a+b） ⁿ的系数。而第n行左手从0开始第j个数值正好等于n！/［j！（n－j）！］。

点数问题对概率论的发展至关重要，尤其是运用到机遇游戏（投资）中。我们回忆一下该问题的基本形式。两人各下一定赌注，谁先赢到n点谁赢得赌注。每得一点都能获得一定奖励，而每轮两人输赢的概率是一样的。如果当第一个人赢得x<n点，而第二人赢得y<n点时两人决定停止比赛，那么此时两人各自应该分得多少赌注？

帕乔利（1494）曾提出，假定两人各下注28个金币，n＝6，且两人的点数为（x，y）=（5，3），此时比赛叫停。帕乔利认为，最公平的分法就是按照两人所得点数的比例分配金币。在这里，金币总数为56

个，那么第一个人分得35个金币，第二个人分得21个金币。意大利数学家卡当，亦即有名的罗拉莫·卡达诺

（1501年9月24日—1576年9月21日）曾在1663年出版《论机遇赌博》（Liber de ludo aleae）。后来亨利·古尔德提出了一个更复杂的解决办法。 ^[12]他认为应该按照还没有结束的新比赛的结果来分配赌注。以帕乔利的例子来说，我们可以设想一个A和B两人的新比赛。如果在B赢得3点之前，A先赢得1分，则A赢；否则， B赢。那么在这个新游戏中，两人各自对赌注的贡献是多少？卡当总结说，A投入3×（3＋1）＝12个金币， B投入1×（1＋1）＝2个金币。这样，如果初始赌注为56个金币，那么A应该得到56×（12/14）=48个金币， 而B得到56×（2/14）=8个金币。

帕斯卡三角形

帕斯卡三角形说明了二项树中的再组合问题，在二项树每一个节点的数字等于上一排两个节点数字之和。更为一般的非再组合二项树最早由波菲利（大约在公元234—305）推广开来。他是新柏拉图派哲学

家，在他的著作《范畴导论》（Introduction to the Categories）中用二项树说明了亚里士多德在范畴方面的逻辑论点。在这个二项树中每一个范畴集合都被分为两个互斥的子集。例如：

在帕斯卡三角形中的数字关系的数量开始是无穷尽的。甚至斐波纳契数列也包含在其中。你是否能发现呢？从左边开始，把一直延伸到右上角的对角线上的数字相加。那么就有：1=1，1+1=2，1+2=3， 1+3+1=5，1+4+3=8，以此类推。

帕乔利和卡达诺的方法都不正确。该问题最终在帕斯卡与费马的一次著名通信（1654年）中得到解 决，此次通信被认为是现代概率论的发端。他们提出了数学期望的思想并假定每位参与者获得的金币为倘若比赛尚未结束的情况下他们各自能得到的金币期望值。

费马的方法只需要数数A能获胜的方法或路径个数以及B能获胜的路径数。

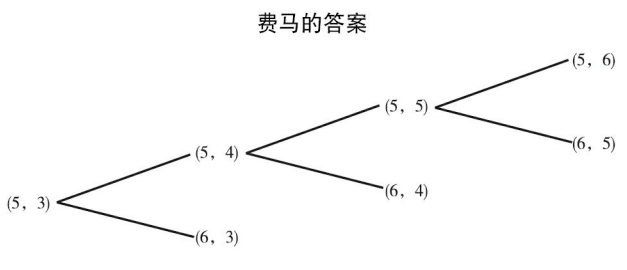
在两位选手得分（5，3）情况下，接下来可能的结果为

（a a a）（a b a）（a b b）（b b a）

（a a b）（b a a）（b a b）（b b b）

其中，a表示第一个选手得一分，b表示第二个选手得一分。加粗的结果意味着第一个选手赢得了比赛。既然在8个可能的结果中有7个是A赢，那么A就应该得到49个金币，而B得到7个。

帕斯卡提出了另一种类似的解决办法，他使用的是反向递归动态规划方法。

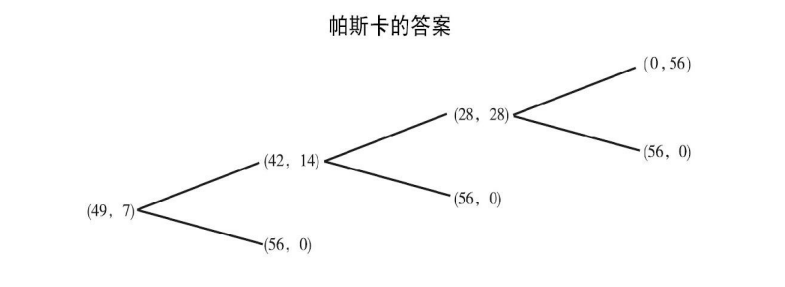
帕斯卡首先问到，如果在双方得分为（5，5）时比赛叫停。由于A和B两人都有平等的机会赢得56个金币，那么他们每人期望得到的是28个金币，赌注是平均分配（28，28）。从这儿往后推，如果得分为（5， 4），再比一轮的话，那么一半的可能是（6，4），赌注分配为（56，0）；另一半的可能是（5，5），这种情况已经阐述，赌注分配为（28，28）。因此，如果得分是（5，4），A得到（1/2）×56＋（1/2）×28＝ 42个金币，B得到（1/2）×0＋（1/2）×28＝14个金币。再往后推一轮到得分为（5，3）的情况，同样的道理可以得到，A分配（1/2）×56＋（1/2）×42＝49个金币，B得到（1/2）×0＋（1/2）×14＝7个金币。 ²

帕斯卡还被誉为决策论的创始人。在他的《思绪》（Pensées）一文中 ^[13]，帕斯卡描述了他著名的“赌注”。他对是否相信上帝的分析十分缜密，让人觉得就应该相信上帝的存在。他说，假设有两种相互排斥的可能性。第一，如果世上没有上帝，那么相信上帝或者不相信上帝都无关紧要。第二，如果真的有上帝， 那么相信上帝会为你带来永生于天堂的无限幸福，而不信上帝则带来葬身于地狱的无尽痛苦。这样，即便你主观地认为存在上帝的概率微乎其微，但只要这个概率大于零，那么你相信上帝所获得的期望收益将会是无穷大。当然，我们现在知道帕斯卡的推理存在严重的问题，因为他的结果取决于他对现实世界可能状态的判断。比如，他忽略了另外一种可能，就是即便存在上帝，信奉者也可能被送进地狱，因为没有人有足够的信息判断他是否真的相信上帝；而怀疑上帝存在的人，在确定的信息下拥有正确的观点从而可能上天堂。

尽管帕斯卡成绩显著，但还称不上是第一位决策理论家。在更早的时候，犹太法典《塔木得9q》

（Kethuboth 9q）就提出，男人不能因为妻子婚前的性行为而与妻子离婚。原因在于，有可能是由于该男人的关系而使妻子发生了婚前性行为；即便不是前一种情况，妻子也可能是在并不情愿的情况下发生婚前性行为。总的来说，四种可能情况中只有一种值得男人与妻子离婚，不值得离婚的情况占了多数，因而法律上不允许。帕斯卡赌注可能是“施蒂格勒取名法则”的又一例证。因为在公元303年阿诺庇乌在其著作《反对异教徒》（The Case against the Pagans）中（第2卷第4章）就描述过类似的选择。

作为现代概率论产生的一个重大特征，帕斯卡也许是不自觉地同时运用了概率论的二元性：一方面， 用概率来解释类似于抛硬币以及赌博游戏等物理过程。在这类过程中，概率可以无争议地确定（客观概 率），犹如我们在点数问题中所看见的。另一方面，还可以用概率来解释不可重复事件。在这类事件中， 人们对事件发生的概率大小往往存在较大争议（主观概率），犹如我们在帕斯卡赌注中看见的。因此，有人如萨维奇（1954）在《统计学基础》一书中就提出，利用本适合于非重复事件的主观概率使得人们无法在备选方案中做出理性选择。但是萨维奇的分析只在一种情况下成立，即针对备选方案的打赌是切实可行的，决定打赌结果的事件是可观测的。比如，我们就人死之后的结果进行打赌就是有问题的：即便相信死后没有生命的一方获胜，他也没办法在死后亲自接受赌注。

在20世纪后半叶，数字计算机对投资理论的进一步发展起到至关重要的作用。不管是利用数据库进行经验验证，还是通过数值分析解决数学问题，都需要计算机的帮助。我们其实在相当长的时间内使用了简易计算器，如公元前3000年人们使用的算盘。计算尺大约在1630~1632年就发明出来。在1642~1644年，为科学做出诸多贡献的帕斯卡当时只有20岁左右，他就成功发明了第一台数字计算机。帕斯卡的计算机是通过转动转盘来输入数字，通过齿轮来完成加减法。当你拨动数字时，里面的齿轮就会移动。运算结果显示在键盘上方的窗口。我们可以在巴黎的法国国立工艺学院看到帕斯卡签名的1652年版计算机。如果你到伦敦比较方便，那么你可以在南肯辛顿的科学博物馆看到该计算机的复制品。